HEC-RAS DAM BREAK MODEL

Dam break modelling can be carried out by either i) scaled physical hydraulic models or ii) mathematical simulation using a computer. A modem tool to deal with this problem is the mathematical model, which is most cost effective and approximately solves the governing flow equations of continuity and momentum by computer simulation, as shown in Fig. 1. Mathematical modelling of dam breach floods can be carried out by either one dimensional analysis or two dimensional analysis. In one dimensional analysis, the information about the magnitude of flood, i.e., discharge and water levels, variation of these with time and velocity of flow through breach can be obtained in the direction of flow. In the case of two dimensional analysis, the additional information about the inundated area, variation of surface elevations and velocities in two dimensions can also be predicted. One-­dimensional analysis is generally adopted when valley is long and narrow and the flood wave characteristics over a large distance from the dam are of main interest. The basic theory for dynamic routing in one-dimensional analysis consists of two partial differential equations originally derived by Barre De Saint Venant in 1871. The equations are:

Conservation of mass (continuity) equation

(∂Q/∂X) +∂(A + Ao) / ∂t - q = 0                                                                                (2.1)

Conservation of momentum equation

(∂Q/∂t) + {∂(Q²/ A)/∂X } + g A ((∂h/∂X ) + Sf + Sc ) = 0                                         (2.2)

where Q = discharge, A = active flow area, Ao = inactive storage area, h = water surface elevation, q= lateral outflow, x = distance along waterway, t = time, Sf = friction slope, Sc = expansion contraction slope, and g = gravitational acceleration.

2.0 MODEL SELECTION

Selection of an appropriate model to undertake dam break flood modelling is essential to ensure the right balance between modelling accuracy and cost in terms of time spent developing the model setup. In the present study, HEC­RAS version 4.1.0 model developed by Hydrologic Engineering Center of U. S. Army Corps of Engineers has been selected. HEC-RAS is an integrated system of software, designed for interactive use in a multitasking environment. The system comprises a graphical user interface, separate hydraulic analysis components, data storage and management capabilities, graphics and reporting facilities. The model contains advanced features for dam break simulation.

The present version of HEC-RAS system contains two one-dimensional hydraulic components for: i) Steady flow surface profile computations; ii)
unsteady flow simulation. The steady/unsteady flow components are capable of modelling sub critical, super critical, and mixed flow regime water surface profiles. The system can handle a full network of channels, a dendric system, or a single river reach. The basic computational procedure is based on the solution of one-dimensional energy equation. Energy losses are evaluated by friction (Manning's equation) and contraction/expansion (coefficient multiplied by the velocity head). The momentum equation is utilized in situations where the water surface profile is rapidly varied.

The graphics include X- Y plots of the river system, schematic cross ­sections, profiles, rating curves, hydrographs, and many other hydraulic variables. Users can select from pre-defined tables or develop their own customized tables. All graphical and tabular output can be displayed on the screen, sent directly to a printer, or passed through the Windows clipboard to other software's, such as word processor or spread sheet. Reports can be customized taking into account the amount and type of information desired.

2.1 MODEL STABILITY DURING UNSTEADY FLOW SIMULATION

HEC-RAS uses an implicit finite difference scheme. The common problem of instability in the case of unsteady flow simulation can be overcome by­ suitable selection of following:

• Cross-section spacing along the river reach
• Computational time step
• Theta weighing factor for numerical solution
• Solution iterations
• Solution tolerance
• Weir and spillway stability factors

2.1.1 Cross-section spacing

The river cross-sections should be placed at representative locations to describe the change in geometry. Additional cross-sections should be added
at locations where changes occur in discharge, slope, velocity and roughness to describe the change in geometry. Cross-sections must also be added at levees, bridges, culverts, and other structures. Bed slope plays an important role in deciding the cross-section spacing. Streams having steep slope require cross- sections at a closer spacing say 100 m or so. For larger uniform rivers with flat slope, the cross- section spacing can vary from 200 m to 500 m.

2.1.2 Computational Time Step

Stability and accuracy can be achieved by selecting a computational time step that satisfies the Courant condition: Cr = Vw(Δt/Δx) ≤ 1.0. Therefore, Δt ≤ Δx/Vw ), where V w = flood wave speed, V = average velocity of flow, Δx = distance between cross sections, and Δt = computational time step. For most of the rivers, the flood wave speed (Vw) can be calculated as: Vw = dQ/dA, where dQ is the change in discharge with change in cross-sectional area (dA). However, an approximate way of calculating flood wave speed (Vw) is to multiply the average speed (V) by a factor. Factors for various channel shapes are shown in Table 2.1 below:

Table 2.1 Ratio of wave speed (V w) to average velocity (V) for various channel shapes

 

Channel Shape		Ratio (Vw/V)
Wide rectangular		1.67
Wide parabolic		1.44
	-
Triangular		1.33
Natural Channel		1.50

 

2.1.3 Theta Weighing Factor

Theta is a weighing factor applied to the finite difference approximations when solving the unsteady flow equations using an implicit scheme.
Theoretically, Theta can vary from 0.5 to 1.0. Theta of 1.0 provides most stability, while Theta of 0.6 provides most accuracy.

2.1.4 Solution Iteration

At each time step, derivatives are estimated and the equations are solved. All the computational nodes are then checked for numerical error. If the error is
greater than the allowable tolerances, the program will iterate. The default number of iterations in HEC-RAS is set to 20. Iterations are for improving the solution.

2.1.5 Solution tolerances

Two solution tolerances can be set or changed by the user: i) water surface calculation and ii) storage area elevation. Making the tolerance larger can reduce the stability problem. Making them smaller can cause the program to go to the maximum number of iterations every time.

2.1.6 Weir and spillway stability factor

Weirs and spillways can often be a source of instability in the solution. During each time step, the flow over a weir/spillway is assumed to be constant. This can cause oscillations by sending too much flow during a time step. One solution is to reduce the time step.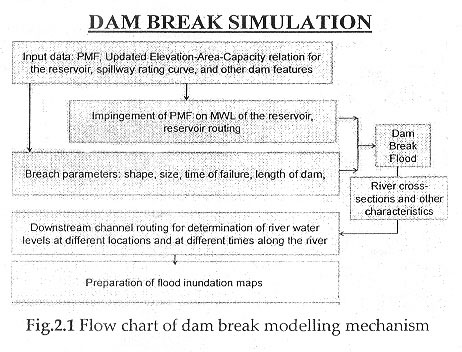


'­

2.2 MODEL LIMITATIONS

The water in HEC-RAS modelling has been assumed to flow in the longitudinal direction only, i.e. the flow is one-dimensional implying that there is no direct modelling of the hydraulic effects of cross-section shape changes, bends, and other two and three-dimensional aspects of flow. It represents the terrain as a sequence of cross-sections and simulate flow to estimate the average velocity and water depth at each cross-section. The
uncertainties associated with the breach parameters, specially breach width, breach depth and breach development time may cause uncertainty in flood peak and arrival time. Further, the high velocity flows associated with dam break floods can cause significant scour of channels. This enlargement in channel cross-section is neglected since the equations for sediment transport, sediment continuity, dynamic bed form friction etc. are not included in the governing equations of the model. The narrow channels with minimal flood planes are subject to over-estimation of water elevation due to significant channel degradation. The dam breach floods create a large amount of transported debris, which may accumulate at very narrow cross sections, resulting in water level variation at downstream locations. This aspect has been neglected due to limitations in modelling of such complicated physical process.

2.3 INPUT DATA REQUIREMENT

In general, the data required for dam break analysis can be categorized as described below.

2.3.1 Reservoir data

To predict the flood hydrograph from the reservoir, it is necessary to have either of the following along with details of typical flow through the reservoir and normal retained water level.

• A elevation- storage relationship for the reservoir, or
• Bathymetric data for the reservoir

Provision of just an elevation-area or elevation-volume relationship limits the extent of modelling possible to predict flood flow out of the reservoir. Under these conditions, only a simple 'flat pond' can be modelled which does not take into consideration the time taken for flow to exit the reservoir. This may be significant if the reservoir is relatively long and narrow or has number of branches.

2.3.2 Catchment hydrology

Inflow into the reservoir, reservoir condition at the time of failure and base flow conditions in the river valley downstream may combine to have a significant effect on the predicted flood conditions, depending on the size and nature of the reservoir and dam. Potential reservoir inflow and river base flow data should be collected to allow a sensitivity analysis to be undertaken as part of the dam break analysis. For high-risk sites, it is likely that the flow conditions assumed for the sensitivity analysis would range from normal low flow operating conditions to a probable maximum flood (PMF).

2.3.3 Structural data

A minimum of information is required to allow a reasonable prediction of breach size, and hence, potential flood flow in the event of structure failure.
Regardless of structure type, it is necessary to outline structure dimensions and levels. Details of gates, valves, and spillways will be required, if partial failure modes are to be considered, and as part of a sensitivity analysis when considering different reservoir/ river water levels and base flow conditions at the time of failure. Techniques for the prediction of breach formation through embankment dams are more advanced than techniques for the prediction of concrete or masonry structure failure. For embankment dams, details of core and layer geometry (including any surface protection) along with respective material sizes will be required. For concrete and masonry structures, the potential failure mechanisms will be based either on potential maximum breach dimensions or failure of single units such as buttresses or spillways. General arrangement drawings ror the structure should provide sufficient information to allow such an analysis.

2.3.4 Topographic data

Topographic data representing the whole area potentially liable to flooding is required. The extent of this data should not be underestimated. Floods
resulting from dam failure can be significantly larger than natural floods-- ­meaning that flood flow is often through areas considered safe from flooding view-point. Required topographic data will therefore extend widely across floodplains and up-valley slopes well above normal flood levels.

Details of major structures that may form an obstruction to flow are also required, such as road and railway embankments and bridges and-major river control structures. Contrary to river modelling studies, smaller  structures that may be completely inundated, and therefore, washed away, may be ignored for dam break modelling purposes.

The accuracy of a dam break study is different from that of a river modelling study. Traditional river modelling simulates natural floods that occur within defined floodplain areas. Our knowledge of typical flow conditions and modelling parameters such as channel and floodplain roughness for these events is relatively good. Equally, there is likely to be a range of data available with which the model may be calibrated. For a dam break model the flow conditions typically exceed natural events by a large margin meaning that there is little calibration data and the flooded terrain is outside of the normal floodplain areas making the estimation of channel roughness difficult. Equally, there is uncertainty in prediction of the failure mechanisms leading to the initial flood hydro graph, in understanding 3D flow effects and in predicting the movement and impact of debris and sediment. With this range of uncertainty, it is inappropriate to attempt flow modelling to the same level of accuracy as for normal river flow modelling. The accuracy of topographic data collected should also relate to the location within the area at risk.

Thus, in brief, the following data are required for a typical dam break analysis:

• Salient features of dam and other hydraulic structures in study reach of the river.
• Rating curves of all the hydraulic structures in the study reach of the river
• Design flood hydrograph.
• Spillway rating curve.
• Cross-sections of the river from dam site to the most downstream location of interest.
• Elevation - storage/area relationship of the reservoir.
• Stage-discharge relationship at the last river cross-section of the study area, if available.
• Manning's roughness coefficient for different reaches of the river under study.
• Topographic map of the downstream area at a scale of 1:15000 to 1:25000, with a contour interval of 2 to 5 m for preparation of inundation map for dam break flood.
• Breach Geometry.
• Time taken for Breach formation.
• Reservoir elevation at start of failure and initial water elevation.
•  Description of d/s flow condition, i.e. subcritical and super-critical.